テンセグイティー その３

テンセグリィーの現状例

テンセグリィーの概念は、今やフラーやスネルソンを離れかなり広がりを見せています。

たとえば、以下のサイトで示されている様な生態学的な研究の成果です。

• http://www.intensiondesigns.com/
• http://www.anatomytrains.com/uploads/rich_media/AnatomyTrainsOverview.pdf

もちろん、ドーム建築への適用はフラーの直弟子といわれる梶川泰司氏によって、引き継がれています。
フラーの影響が強いせいもあって、その幾何範囲は、プラトン立体を基点とするジオデシック幾何（球面幾何）の範疇に収まっているように見受けられます。
しかし、彼の特許文献で示された、折り畳み式展開可能のジオデシックタイプのテンセグリティードームの発想は、フラーでは出来なかったドームを発展した点で大変評価できると思います。

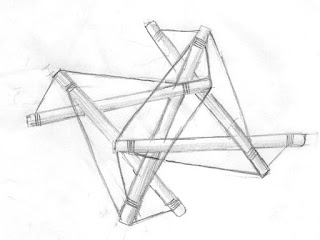
梶川泰司によるテンセグリティーモジュール

それによるテンセグリティードーム

テンセグリィーの分類

さて、これから示していく方向をざっと明確にしていくため、右のようなシェーマ図を描いてみました。
テンセグリティーにも色々あり、プラトン立体を中心にすると以下の様な関係となり、Ａ，Ｂ，Ｃの三つに大別できます。

Ｃは、上位概念に含まれるもので、場合によってはテントやマストといった類も含みます。
Ｂは、球面幾何によって形作られるもので、ジオデシック理論によるドーム型のタイプです。
Ａは、テンセグリティー模型でよくお目にかかるもので、プラトン立体に準じるものです。これについては後に紹介しましょう。

説明を加えますと、先ほどの最初に取り上げた生態学的なものは、ほとんどＣに含まれるといってよいでしょう。

フラーや梶川氏のジオデシック理論による球形やドーム型のドームなどはＢに入ります。

また、両者は正多面体を基にその連続体も試みているので、それらはＡに入ります。

もとより、ジオデシック理論は球面を正多面体の性質を利用して分割しているのでＡ＋Ｂに入れてよいでしょう。

ケネス・スネルソンはＢを抜かしてＡにおいて連続体に挑み、Ｃにおいては、正多面体の呪縛を逃れ、飛躍した展開を見せています。

いずれにせよ、Ａの領域はプラトン立体の呪縛が強いため、デザインへの技術転換は容易ではありません。この手の領域を扱うデザイナーの第一の難関です。

フラーにせよ、スネルソンにせよ、何らかの要素を原基であるプラトン立体に持ち込み変容させてきました。
フラーの場合、それが球面幾何であり、スネルソンの場合は独自の造形力と解析方法を編み出した点にあります。

ここで開示していく内容は、両者に共通する点もありますが、まったく異なる方法によるものです。
それは、プラトン立体をより深く掘り下げることで見えてきます。

次回、テンセグリティーとプラトン立体の関係に入っていきたいと思います。

テンセグイティー その２

テンセグリティーへの入口


本格的なテンセグリティーといえば、軸材と線材が複雑に張り合って形がつかみにくいものがほとんどです。
実際に面からなる立体とはかなり違い、感覚的についていけないものが多くあります。

しかし、そのような複雑なものでも、ごく単純なパターンの繰り返しであったり、バリエーションの組み合わせだったりするものです。

そこで先ず、単純なところから入っていこうと思います。
テンセグリティーの上位概念から入っていきましょう。
この時点で明確な定義は必要ありません。

その単純な例に弓があります。
弓は、弦の張りと弓本体のしなりという２つの要素が一つになることで成り立ってます。

この弓の弦にもう一本の別の弓の端をつなぎ、このパターンを繰り返して三角形を作ってみます。

こうすることで三角形の面にあわせたパターンができます。こういったのを一つの単位とみなしてモジュールと呼んでます。
このモジュールをつなげて骨組みをつくろうなどと考えれば弓では柔軟すぎて何も支えれません。

そこでヨットのマストとロープの要素を取り出して同様に考えて見ましょう。
マストの端をロープに固定し、ずれないものと仮定します。
このようにしてできた三角形は弓よりかたちを保ちやすいですが、このモジュールだけではぐらつきます。

平面がそれ自身で自立しないのと同様このモジュールも床に倒れたままです。立体にならってつなげて行けば自立して崩れない骨組みを作ることができるはずです。

三角形で出来るもっと単純な形の正四面体を選んでみましょう。
この立体の面にあわせて先のモジュールを置いていきます。
立体の場合、それぞれの面が隣り合う面と辺を共有しています。

同様に、テンセグリティーもそのマストを共有しながら連結していきます。
一つの辺を共有して二つの面が連結するのと同様、一つのマストを共有して２つのモジュールが連結します。
したがって、一つのマストには必ず2本の張り材が張られ、２本のマストが左右から重なり合います。

この性質は、テンセグリティーのもっとも知られた形態、すなわちフラーやスネルソンが行なった形態に共通の特徴です。

さて、このモジュールを引き続き正四面体にならってつなげていきましょう。
かなり面の場合と違って、からみがちになりますが、手順はワンパターンです。
これは手元で模型を作る際には紐の変わりに輪ゴムが適しています。


右のようなマストの構成ができます。相対するマストがそれぞれ平行に配置してます。
この場合、マストとロープの長さはある程度直感で導くことができます。
それにはある規則性がありますが、この段階ではそれについては触れる必要はないでしょう。。
それぞれの長さなどは適当に調整すれば骨組みの強度は保たれるのです。

スネルソンもフラーもこの段階から入っていきました。
試行錯誤と直感で望んでいったことでしょう。
フラーのテンセグリティーの特徴はこのモジュールをジオデシックドームに習って構成したことです。
一方、スネルソンは立体にはならっていますが、立体をゆがませる計算を発見したといってよいでしょう。
フラーは結局規則性が見つけられずにいたのではないかと思います。
テンセグリティーをジオデシック球に展開していくとテンセグリティーの規則性が見つけにくいのです。

次回、何とかその規則性の方向に話の流れをもって行きたいと思ってます。

テンセグリティー その１

　テンセグリティーといえば、フラーや彫刻家のスネルソンが手をつけていたことで知られてます。
どちらの発明かというと、正確にはスネルソンが始めてフラーが触発され、発明・公認好きのフラーが特許登録しています。だからかなり法的に争っていたようです。
私は、スネルソンの方がテンセグリテーの専門家だと思う。実際作品がそれを語っている。しかも彼はそれをランドスケープに限って展開していました。

一方、フラーの方は具体的な構造物として実現してはいなかったようですが、実験や著作による思想性が後の人に影響を与えた様です。

そのテンセグリティー、一般には分かりにくい。しかも建築や構造以外に医学の分野でも取り上げられ人体と関係があるらしい。
私のサイトにもテンセグリティーを探しに来る人がかなりいる。
しかし実際、触れる程度の内容です。
そこで、今後しばらくはテンセグリテーとは何かについて具体的に示そうと思っています。
なぜなら、それは構造の通常と異なる概念であり、今後触れることになる第三の構造を変容したものでもあるからです。それに、その内容は他にも異なる分野で役立つような気もするのです。

ジャコメッティという彫刻家がいて、人体を極限まで細くすることで人の本質を見い出そうとした作家がいます。第三の構造については、まだその全容まで示してませんが、同様に極限まで細くすることでその構造の本質というか別の面が見えてくるようにも思うのです。

次回、模型と絵図で説明できたらと思っています。