1.jpg)
テンセグリティーへの入口
本格的なテンセグリティーといえば、軸材と線材が複雑に張り合って形がつかみにくいものがほとんどです。
実際に面からなる立体とはかなり違い、感覚的についていけないものが多くあります。
しかし、そのような複雑なものでも、ごく単純なパターンの繰り返しであったり、バリエーションの組み合わせだったりするものです。
その単純な例に弓があります。
弓は、弦の張りと弓本体のしなりという2つの要素が一つになることで成り立ってます。
弓は、弦の張りと弓本体のしなりという2つの要素が一つになることで成り立ってます。
この弓の弦にもう一本の別の弓の端をつなぎ、このパターンを繰り返して三角形を作ってみます。
こうすることで三角形の面にあわせたパターンができます。こういったのを一つの単位とみなしてモジュールと呼んでます。
このモジュールをつなげて骨組みをつくろうなどと考えれば弓では柔軟すぎて何も支えれません。
そこでヨットのマストとロープの要素を取り出して同様に考えて見ましょう。
マストの端をロープに固定し、ずれないものと仮定します。
 このようにしてできた三角形は弓よりかたちを保ちやすいですが、このモジュールだけではぐらつきます。
このようにしてできた三角形は弓よりかたちを保ちやすいですが、このモジュールだけではぐらつきます。
平面がそれ自身で自立しないのと同様このモジュールも床に倒れたままです。立体にならってつなげて行けば自立して崩れない骨組みを作ることができるはずです。
三角形で出来るもっと単純な形の正四面体を選んでみましょう。
この立体の面にあわせて先のモジュールを置いていきます。
立体の場合、それぞれの面が隣り合う面と辺を共有しています。
同様に、テンセグリティーもそのマストを共有しながら連結していきます。
一つの辺を共有して二つの面が連結するのと同様、一つのマストを共有して2つのモジュールが連結します。
したがって、一つのマストには必ず2本の張り材が張られ、2本のマストが左右から重なり合います。
この性質は、テンセグリティーのもっとも知られた形態、すなわちフラーやスネルソンが行なった形態に共通の特徴です。
さて、このモジュールを引き続き正四面体にならってつなげていきましょう。
かなり面の場合と違って、からみがちになりますが、手順はワンパターンです。
これは手元で模型を作る際には紐の変わりに輪ゴムが適しています。

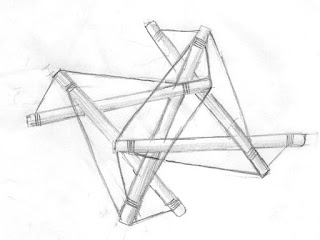
右のようなマストの構成ができます。相対するマストがそれぞれ平行に配置してます。
この場合、マストとロープの長さはある程度直感で導くことができます。
それにはある規則性がありますが、この段階ではそれについては触れる必要はないでしょう。。
それぞれの長さなどは適当に調整すれば骨組みの強度は保たれるのです。
スネルソンもフラーもこの段階から入っていきました。
試行錯誤と直感で望んでいったことでしょう。
フラーのテンセグリティーの特徴はこのモジュールをジオデシックドームに習って構成したことです。
一方、スネルソンは立体にはならっていますが、立体をゆがませる計算を発見したといってよいでしょう。
フラーは結局規則性が見つけられずにいたのではないかと思います。
テンセグリティーをジオデシック球に展開していくとテンセグリティーの規則性が見つけにくいのです。
次回、何とかその規則性の方向に話の流れをもって行きたいと思ってます。
このモジュールをつなげて骨組みをつくろうなどと考えれば弓では柔軟すぎて何も支えれません。
そこでヨットのマストとロープの要素を取り出して同様に考えて見ましょう。
マストの端をロープに固定し、ずれないものと仮定します。
 このようにしてできた三角形は弓よりかたちを保ちやすいですが、このモジュールだけではぐらつきます。
このようにしてできた三角形は弓よりかたちを保ちやすいですが、このモジュールだけではぐらつきます。平面がそれ自身で自立しないのと同様このモジュールも床に倒れたままです。立体にならってつなげて行けば自立して崩れない骨組みを作ることができるはずです。
三角形で出来るもっと単純な形の正四面体を選んでみましょう。
この立体の面にあわせて先のモジュールを置いていきます。
立体の場合、それぞれの面が隣り合う面と辺を共有しています。
同様に、テンセグリティーもそのマストを共有しながら連結していきます。
一つの辺を共有して二つの面が連結するのと同様、一つのマストを共有して2つのモジュールが連結します。
したがって、一つのマストには必ず2本の張り材が張られ、2本のマストが左右から重なり合います。
この性質は、テンセグリティーのもっとも知られた形態、すなわちフラーやスネルソンが行なった形態に共通の特徴です。
さて、このモジュールを引き続き正四面体にならってつなげていきましょう。
かなり面の場合と違って、からみがちになりますが、手順はワンパターンです。
これは手元で模型を作る際には紐の変わりに輪ゴムが適しています。
右のようなマストの構成ができます。相対するマストがそれぞれ平行に配置してます。
この場合、マストとロープの長さはある程度直感で導くことができます。
それにはある規則性がありますが、この段階ではそれについては触れる必要はないでしょう。。
それぞれの長さなどは適当に調整すれば骨組みの強度は保たれるのです。
スネルソンもフラーもこの段階から入っていきました。
試行錯誤と直感で望んでいったことでしょう。
フラーのテンセグリティーの特徴はこのモジュールをジオデシックドームに習って構成したことです。
一方、スネルソンは立体にはならっていますが、立体をゆがませる計算を発見したといってよいでしょう。
フラーは結局規則性が見つけられずにいたのではないかと思います。
テンセグリティーをジオデシック球に展開していくとテンセグリティーの規則性が見つけにくいのです。
次回、何とかその規則性の方向に話の流れをもって行きたいと思ってます。
1.jpg)
2.jpg)

0 件のコメント:
コメントを投稿